4196번: 도미노
도미노는 재밌다. 도미노 블록을 일렬로 길게 늘어세운 뒤 블록 하나를 넘어뜨리면 그 블록이 넘어지며 다음 블록을 넘어뜨리는 일이 반복되어 일렬로 늘어선 블록들을 연쇄적으로 모두 쓰러
www.acmicpc.net
4196번 : 도미노
도미노는 재밌다. 도미노 블록을 일렬로 길게 늘어세운 뒤 블록 하나를 넘어뜨리면 그 블록이 넘어지며 다음 블록을 넘어뜨리는 일이 반복되어 일렬로 늘어선 블록들을 연쇄적으로 모두 쓰러뜨릴 수 있다. 그러나, 가끔씩 도미노가 다른 블록을 넘어뜨리지 못하게 배치되어 있다면, 우리는 다음 블록을 수동으로 넘어뜨려야 한다.
이제 각 도미노 블록의 배치가 주어졌을 때, 모든 블록을 넘어뜨리기 위해 손으로 넘어뜨려야 하는 블록 개수의 최솟값을 구하자.
입력
첫 번째 줄에 테스트 케이스의 개수가 주어진다.
각 테스트 케이스의 첫 번째 줄에는 두 정수 N, M이 주어지며 두 수는 100,000을 넘지 않는다. N은 도미노의 개수를, M은 관계의 개수를 나타낸다. 도미노 블록의 번호는 1과 N 사이의 정수다. 다음 M개의 줄에는 각각 두 정수 x, y가 주어지는데, 이는 x번 블록이 넘어지면 y번 블록도 넘어짐을 뜻한다.
출력
각 테스트 케이스마다 한 줄에 정수 하나를 출력한다. 정답은 손으로 넘어뜨려야 하는 최소의 도미노 블록 개수이다.

생각해 볼 점
SCC 문제입니다.
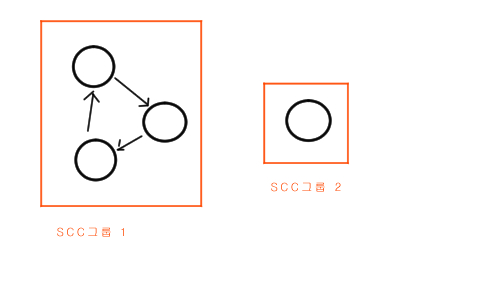
우선, SCC의 그룹을 만들어 줍니다.
잘 생각해보면 SCC의 그룹은 그룹 내 어떤 도미노를 넘어뜨려도
반드시 그 그룹의 모든 도미노가 쓰러진다는 특징이 있습니다.
따라서, SCC 그룹을 하나의 도미노 그룹이라 생각하고,
그룹 당 손으로 넘어뜨리는 횟수 1회라고 생각하면 편합니다.
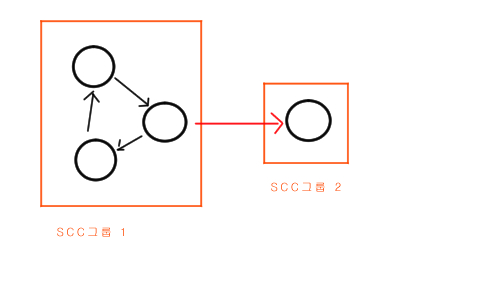
그런데, 그룹들 사이에 다음처럼 간선이 존재한다면, 1그룹을 넘어뜨리면 2그룹도 넘어지므로
횟수는 2회에서 1회로 감소할 것입니다.
즉, SCC그룹을 하나의 그래프로 생각하여 위상정렬 알고리즘까지 적용하면,
횟수를 정확하게 구해낼 수 있을 것입니다.
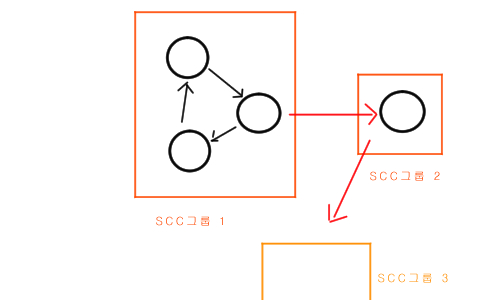
위와 같은 간선을 가질 경우, SCC1 그룹 중 아무거나 넘어뜨리면 3번까지 1번에 모두 넘어집니다.

이 경우는 좀 다릅니다. 1그룹과 3그룹을 모두 손으로 쓰러뜨려야 모든 도미노가 넘어집니다.
즉, 위상정렬 알고리즘과 동일하게,
들어오는 간선이 0개인 SCC그룹의 갯수를 세면 그것이 정답이 됩니다.
들어오는 간선이 있다는 것은 곧, 이전 SCC그룹이 넘어지면 같이 넘어진다는 뜻이고,
들어오는 간선이 없다는 것은, 자신을 넘어뜨려 줄 SCC 그룹이 없다는 뜻이므로,
손으로 넘어뜨려주는 수 밖에 없기 때문입니다.
코드
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
//정방향 DFS, Stack을 채워오는 용도
void dfs(bool *&visited, vector<int> *&edges, stack<int> &st, int const ¤t)
{
if (visited[current]) return;
visited[current] = true;
for (int next : edges[current])
{
if (visited[next]) continue;
dfs(visited, edges, st, next);
}
st.push(current);
}
//역방향 DFS, SCC그룹을 확정짓는 용도
void dfs(bool*& visited, vector<int>*& edges, int const& current)
{
if (visited[current]) return;
visited[current] = true;
for (int next : edges[current])
{
if (visited[next]) continue;
dfs(visited, edges, next);
}
}
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
int N, M;
scanf("%d %d", &N, &M);
bool* visited = new bool[N];
vector<int>* edges = new vector<int>[N];
vector<int>* rev_edges = new vector<int>[N];
for (int i = 0; i < M; i++)
{
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
edges[a].push_back(b);
rev_edges[b].push_back(a);
}
//코사라주 알고리즘
stack<int>st;
fill_n(visited, N, false);
for (int i = 0; i < N; i++)
{
if (visited[i]) continue;
dfs(visited, edges ,st ,i);
}
int ans = 0;
fill_n(visited, N, false);
while (!st.empty())
{
int current = st.top();
st.pop();
if(visited[current]) continue;
dfs(visited, edges, current);
ans++;
}
printf("%d\n", ans);
delete[] visited;
delete[] edges;
delete[] rev_edges;
}
return 0;
}
그 외
사실 제 코드에서는 indegree를 이용하고 있지 않은데,
이 문제에서 굳이 SCC 그룹을 구해야한다고 한 적은 없으며,
정방향 DFS를 통해 얻은 Stack에서 가장 위의 노드는 항상 indegree == 0인 노드이며,
이를 역방향 DFS를 돌렸을 때, SCC 그룹마다 ans가 올라가는 구조로 되어있습니다.
따라서, 제 코드 역시 맞는 코드입니다.
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 2845번 문제 (0) | 2021.12.29 |
|---|---|
| [C++]백준 - 2558번 문제 (0) | 2021.12.28 |
| [C++]백준 - 2475번 문제 (0) | 2021.12.26 |
| [C++]백준 -1550번 문제 (0) | 2021.12.25 |
| [C++]백준 - 11724번 문제 (0) | 2021.12.25 |
![[C++]백준 - 4196번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FxIyfQ%2FbtroTdPBeRa%2F6GQwUpVcAgzwIe8krW5yk0%2Fimg.jpg)