1520번: 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으
www.acmicpc.net
1520번 : 내리막 길
여행을 떠난 세준이는 지도를 하나 구하였다. 이 지도는 아래 그림과 같이 직사각형 모양이며 여러 칸으로 나뉘어져 있다. 한 칸은 한 지점을 나타내는데 각 칸에는 그 지점의 높이가 쓰여 있으며, 각 지점 사이의 이동은 지도에서 상하좌우 이웃한 곳끼리만 가능하다.
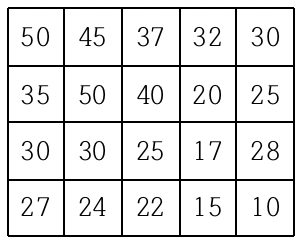
현재 제일 왼쪽 위 칸이 나타내는 지점에 있는 세준이는 제일 오른쪽 아래 칸이 나타내는 지점으로 가려고 한다. 그런데 가능한 힘을 적게 들이고 싶어 항상 높이가 더 낮은 지점으로만 이동하여 목표 지점까지 가고자 한다. 위와 같은 지도에서는 다음과 같은 세 가지 경로가 가능하다.
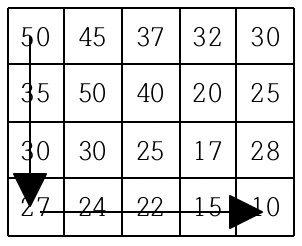
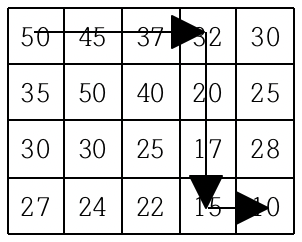

지도가 주어질 때 이와 같이 제일 왼쪽 위 지점에서 출발하여 제일 오른쪽 아래 지점까지 항상 내리막길로만 이동하는 경로의 개수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에는 지도의 세로의 크기 M과 가로의 크기 N이 빈칸을 사이에 두고 주어진다. 이어 다음 M개 줄에 걸쳐 한 줄에 N개씩 위에서부터 차례로 각 지점의 높이가 빈 칸을 사이에 두고 주어진다. M과 N은 각각 500이하의 자연수이고, 각 지점의 높이는 10000이하의 자연수이다.
출력
첫째 줄에 이동 가능한 경로의 수 H를 출력한다. 모든 입력에 대하여 H는 10억 이하의 음이 아닌 정수이다.

생각해 볼 점
"그냥 DFS 문제 아닌가?"라고 생각하기 쉽습니다.
DFS 탐색만으로 문제를 풀면 시간초과가 납니다.
우선, 좌표마다 상 하 좌 우 총 4번을 탐색해야하므로 시간이 많이 걸립니다.
500 * 500정도의 공간이라면 DP를 이용해서 풀 정도의 크기이므로 DP를 이용해 시간을 단축합니다.
DFS의 원리를 사용한 재귀함수로 탐색을 하되, DP를 통해 이전 값의 결과를 이용할 것입니다.
최종 목표 = (N, M)의 경로의 수
Solution(x, y)를 (0,0)에서 (x,y) 좌표까지의 경로의 수라고 가정합니다.
Solution(0, 0) = 1
Solution(x, y) = (x, y 좌표의 상, 하, 좌, 우의 Solution 값을 모두 더한 값)
DP는 Solution의 결과를 담되, 아직 탐색되지 않은 곳은 -1을 저장합니다.

위 그림과 같은 순서로 진행됩니다. Solution(1, 1)을 구하려면, Solution(0,1) + Solution(1, 0)을 구해야 하고, Solution(0, 0)까지 진행하여 값을 반환 받으면 결국 Solution(1, 1) = 2가 됩니다.
코드
#include <iostream>
#include <queue>
using namespace std;
int M, N; //세로, 가로
int **map;
int **dp;
int move_x[4] = {-1, 0, 1, 0};
int move_y[4] = {0, -1, 0, 1};
//0,0 -> (x, y) 지점까지의 경로의 갯수를 반환
int solution(int x, int y)
{
if(map[y][x] == 10001)
{
dp[y][x] = 0;
return 0;
}
if(dp[y][x] > -1) return dp[y][x];
int result = 0;
for(int i = 0; i < 4; i++)
{
int new_x = x + move_x[i];
int new_y = y + move_y[i];
//재귀
if(map[y][x] < map[new_y][new_x]) result += solution(new_x, new_y);
}
dp[y][x] = result;
return result;
}
int main()
{
scanf("%d %d", &M, &N);
//상하좌우 탐색을 의식해 범위값 +2
map = new int*[M + 2];
dp = new int*[M + 2];
for(int i = 0; i < M + 2; i++)
{
map[i] = new int[N + 2];
dp[i] = new int[N + 2];
//범위 밖은 최대값 10000 + 1을 넣어 불가능한 지역으로 만듬
fill_n(map[i], N + 2, 10001);
//탐색되지 않은 장소 = -1을 넣음
fill_n(dp[i], N + 2, -1);
for(int j = 1; 0 < i && i < M + 1 && j < N + 1; j++) scanf("%d", &map[i][j]);
}
//시작점을 1로 저장
dp[1][1] = 1;
cout << solution(N, M);
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 1697번 문제 (0) | 2021.08.08 |
|---|---|
| [C++]백준 - 10942번 문제 (0) | 2021.08.08 |
| [C++]백준 - 1629번 문제 (0) | 2021.08.05 |
| [C++]백준 - 12865번 문제 (0) | 2021.08.05 |
| [C++]백준 - 1912번 문제 (0) | 2021.08.05 |
![[C++]백준 - 1520번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fc6O0Ty%2Fbtra8neyxq7%2FcX19KguNV2WOVIDPzli0q1%2Fimg.jpg)