1799번: 비숍
첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로
www.acmicpc.net
1799번 : 비숍
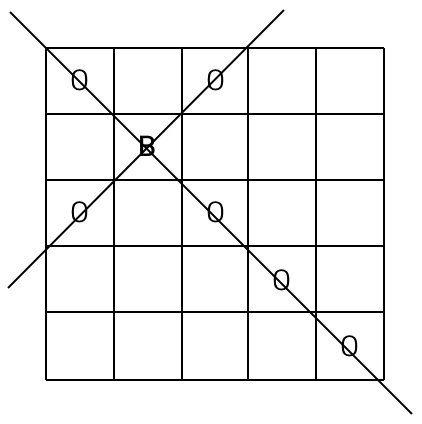
서양 장기인 체스에는 대각선 방향으로 움직일 수 있는 비숍(bishop)이 있다. < 그림 1 >과 같은 정사각형 체스판 위에 B라고 표시된 곳에 비숍이 있을 때 비숍은 대각선 방향으로 움직여 O로 표시된 칸에 있는 다른 말을 잡을 수 있다.
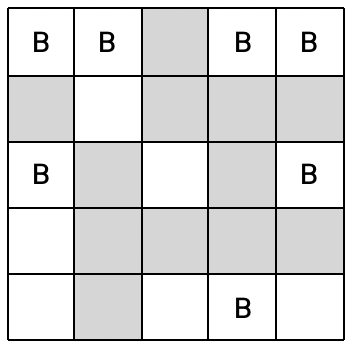
그런데 체스판 위에는 비숍이 놓일 수 없는 곳이 있다. < 그림 2 >에서 체스판에 색칠된 부분은 비숍이 놓일 수 없다고 하자. 이와 같은 체스판에 서로가 서로를 잡을 수 없도록 하면서 비숍을 놓는다면 < 그림 3 >과 같이 최대 7개의 비숍을 놓을 수 있다. 색칠된 부분에는 비숍이 놓일 수 없지만 지나갈 수는 있다.

정사각형 체스판의 한 변에 놓인 칸의 개수를 체스판의 크기라고 한다. 체스판의 크기와 체스판 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 주어질 때, 서로가 서로를 잡을 수 없는 위치에 놓을 수 있는 비숍의 최대 개수를 구하는 프로그램을 작성하시오.
입력
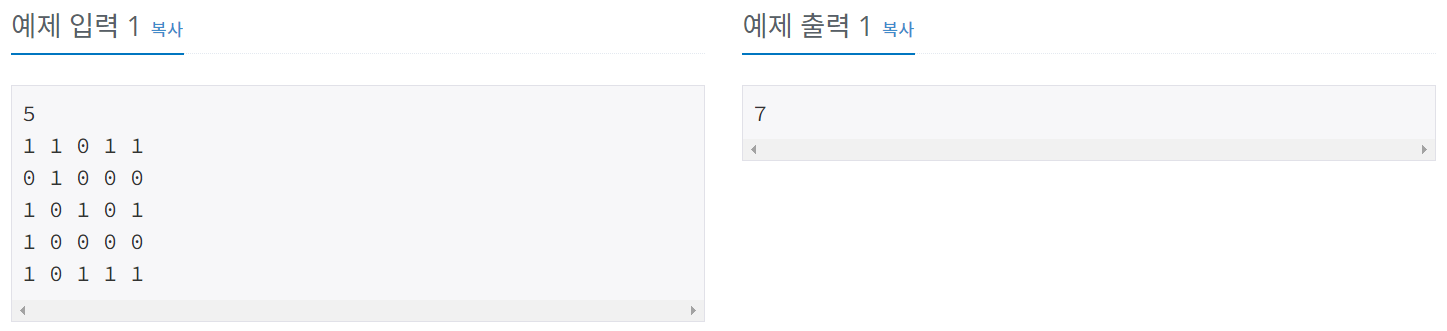
첫째 줄에 체스판의 크기가 주어진다. 체스판의 크기는 10이하의 자연수이다. 둘째 줄부터 아래의 예와 같이 체스판의 각 칸에 비숍을 놓을 수 있는지 없는지에 대한 정보가 체스판 한 줄 단위로 한 줄씩 주어진다. 비숍을 놓을 수 있는 곳에는 1, 비숍을 놓을 수 없는 곳에는 0이 빈칸을 사이에 두고 주어진다.
출력
첫째 줄에 주어진 체스판 위에 놓을 수 있는 비숍의 최대 개수를 출력한다.
생각해 볼 점
백트래킹 문제입니다.
이 문제는 시간초과가 쉽게 납니다.
시간 초과를 피하기 위한 유의사항은 다음과 같습니다.
1. 비숍은 같은 색상의 타일로만 움직일 수 있다.

이는 곧, 검은 비숍과 흰 비숍을 분리하여 백트래킹을 돌릴 수 있다는 뜻입니다.
검은 비숍과 흰 비숍을 분리하면 비약적으로 수행시간이 줄어듭니다.
답 = Solution(Black) + Solution(White)
2. 대각선은 한 그룹으로 묶을 수 있다.
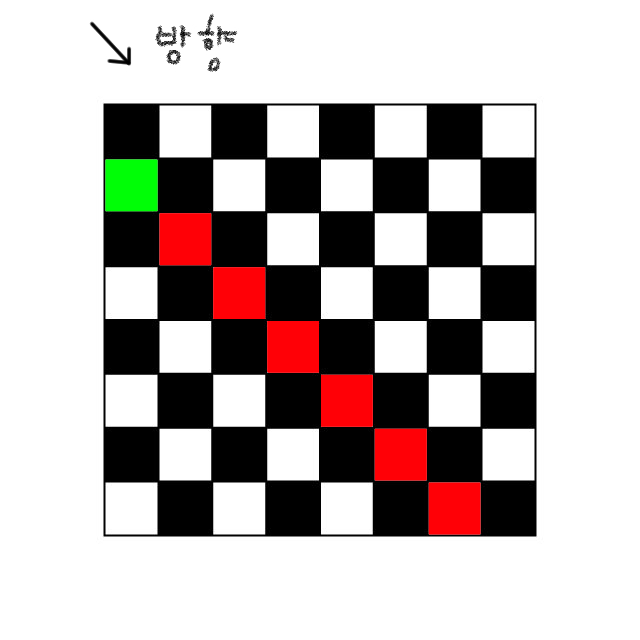
위와 같이 빨간색 칠이 되어있는 \ 방향 대각 타일들은 한 그룹이므로
좌우 끝의 세로 타일만 사용해서 이 그룹이 사용되었는지 체크해줄 수 있습니다.
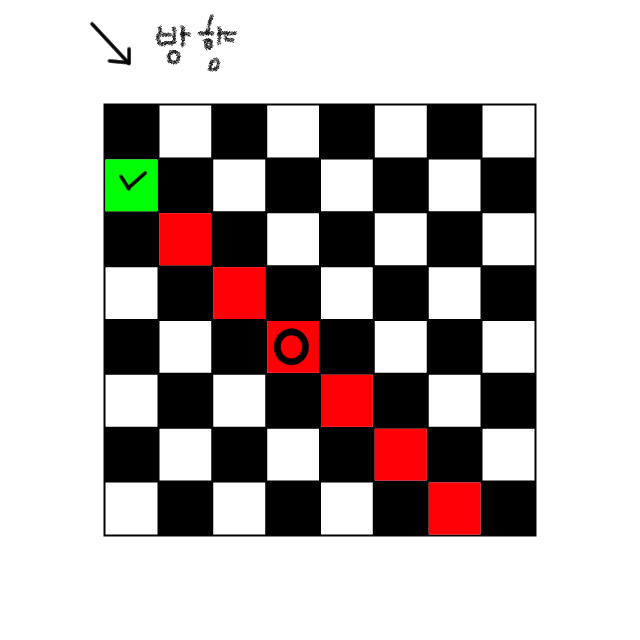
따라서, 붉은 타일 어디든 비숍이 하나 놓인다면, 녹색 타일 index에
이 대각선은 사용할 수 없다고 true 표기를 해놓을 것이고,
그러면 다른 비숍을 놓을 때 이 대각선이 사용 가능한지 단 한칸만 보고도 알수가 있습니다.
다음으로 / 방향 체크는 위 아래 끝 가로 타일만 사용하여 역시 같은 방법으로 해줍니다.

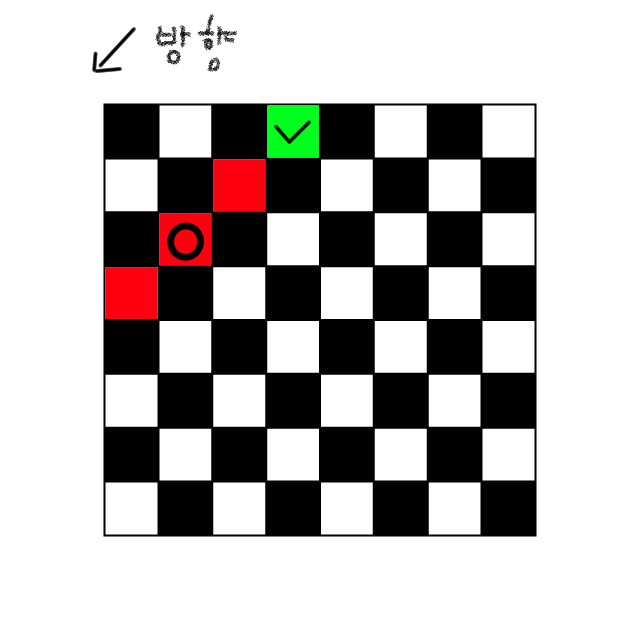
* 계산 방법
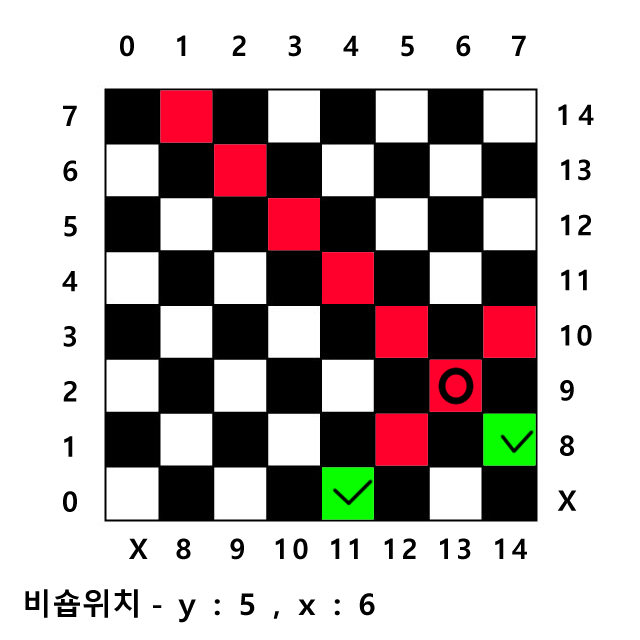
* 현재 비숍 위치의 index 계산식
1. / 방향 : y + x = 11
-> 11번째 Row_index에 체크
2. \ 방향 : N - 1 + x - y = 7 + 6 - 5 = 8
-> 8번째 Col_index에 체크
이 두가지 원리를 사용하여 백트래킹을 돌린다면 시간초과를 피할 수 있습니다.
코드
#include <iostream>
#include <vector>
#define Point pair<int, int>
#define Y first
#define X second
using namespace std;
vector<Point> Bishops[2]; //검은색 흰색 분리
vector<bool> IsPossible_Row;
vector<bool> IsPossible_Col;
//재귀
//BorW == 0 -> Black, BorW == 1 -> White
int Solution(int const& N, int const& prev, int const& count, int const& size, bool const& BorW)
{
if (count == N)
return count;
int ret = count;
for (int i = prev + 1; i < size; i++)
{
int Check_Row = Bishops[BorW][i].Y + Bishops[BorW][i].X;
int Check_Col = N + Bishops[BorW][i].X - Bishops[BorW][i].Y;
if(!IsPossible_Row[Check_Row])
continue;
if(!IsPossible_Col[Check_Col])
continue;
IsPossible_Row[Check_Row] = false;
IsPossible_Col[Check_Col] = false;
ret = max(ret, Solution(N, i, count + 1, size, BorW));
IsPossible_Row[Check_Row] = true;
IsPossible_Col[Check_Col] = true;
}
return ret;
}
int main()
{
int N;
scanf("%d", &N);
for (int y = 0; y < N; y++)
{
for (int x = 0; x < N; x++)
{
int input;
scanf("%d", &input);
if (!input)
continue;
//Black/ White 입력
Bishops[(y + x) & 1].push_back({ y, x });
}
}
IsPossible_Row = vector<bool>(N << 1, true);
IsPossible_Col = vector<bool>(N << 1, true);
int ans = Solution(N, -1, 0, Bishops[0].size(), false);
ans += Solution(N, -1, 0, Bishops[1].size(), true);
printf("%d", ans);
return 0;
}
그 외
이 문제는 풀고나서 고수분들의 풀이를 꼭 한번 참고해보시길 바랍니다.
정말.. 어떻게 이런 생각들을 하는걸까요
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 17299번 문제 (0) | 2022.11.08 |
|---|---|
| [C++]백준 - 2143번 문제 (0) | 2022.11.01 |
| [C++] 백준 - 1238번 문제 (0) | 2022.10.26 |
| [C++]백준 - 1918번 문제 (0) | 2022.10.25 |
| [C++]백준 - 1865번 문제 (0) | 2022.10.21 |
![[C++] 백준 - 1799번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FFMHff%2FbtrQCVBBPph%2FRQ3SgS2Kv5y6P8CPcsJp61%2Fimg.jpg)