1086번: 박성원
첫째 줄에 정답을 기약분수 형태로 출력한다. p/q꼴로 출력하며, p는 분자, q는 분모이다. 정답이 0인 경우는 0/1로, 1인 경우는 1/1로 출력한다.
www.acmicpc.net
1086번 : 박성원
박성원은 이 문제를 풀지 못했다.
서로 다른 정수로 이루어진 집합이 있다. 이 집합의 순열을 합치면 큰 정수 하나를 만들 수 있다. 예를 들어, {5221,40,1,58,9}로 5221401589를 만들 수 있다. 합친수가 정수 K로 나누어 떨어지는 순열을 구하는 프로그램을 작성하시오.
하지만, 박성원은 이 문제를 풀지 못했다.
따라서 박성원은 그냥 랜덤하게 순열 하나를 정답이라고 출력하려고 한다. 이 문제에는 정답이 여러 개 있을 수도 있고, 박성원이 우연히 문제의 정답을 맞출 수도 있다.
박성원이 우연히 정답을 맞출 확률을 분수로 출력하는 프로그램을 작성하시오.
입력
첫째 줄에 집합의 수의 개수 N이 주어진다. N은 15보다 작거나 같은 자연수이다. 둘째 줄부터 N개의 줄에는 집합에 포함된 수가 주어진다. 각 수의 길이는 길어야 50인 자연수이다. 마지막 줄에는 K가 주어진다. K는 100보다 작거나 같은 자연수이다.
출력
첫째 줄에 정답을 기약분수 형태로 출력한다. p/q꼴로 출력하며, p는 분자, q는 분모이다. 정답이 0인 경우는 0/1로, 1인 경우는 1/1로 출력한다.

생각해 볼 점
우선, 입력값의 길이가 50을 넘는 자연수이므로
정수형으로는 받을 수가 없습니다. string을 이용해 수를 받습니다.
그리고, 어차피 우리는 나머지 연산을 이용할 것이므로, string으로 받은 입력 값을
K로 나눈 나머지로 저장합니다.
그런데, 우리는 입력값을 이어 붙인 수열이 어떻게 나누어 떨어질 지 아닐지 알 수가 있을까요?
예를들어, 4와 27을 입력받았습니다. 그리고 K = 7입니다.
4와 27을 이어붙여 427의 수를 만들었고, 7로 나누어 떨어지는 지 알고 싶습니다.
427 % 7 = 0입니다.
하지만, 4와 27만으로도 나누어 떨어지는 지 알 수 없을까요?
4 % 7 = 3
27 % 7 = 6입니다.
이걸 자리수에 맞게 이어붙여 봅시다.
원래 4 와 27을 이어 붙일 때
4 * 100 + 27이었습니다.
그러므로, 우리는 나머지 연산을 다음과 같이 진행한 셈입니다.
427 % 7 == ( (4 % 7 * 100 % 7) % 7 + (27 % 7) ) % 7
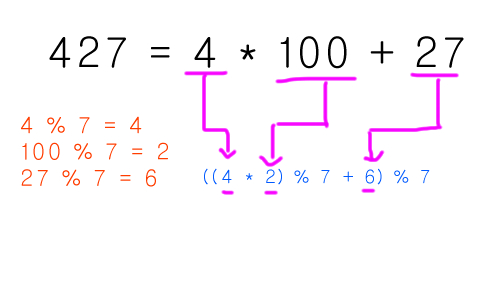
그러므로, 우리는 입력값에 대한 자릿수도 같이 저장해 주어야 합니다.
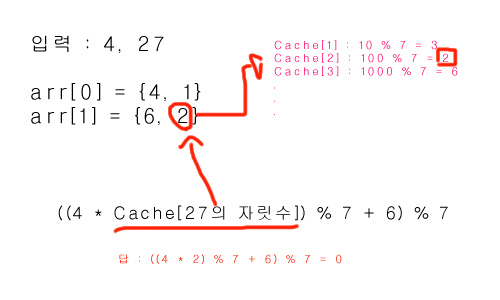
4와 27이 입력이라면 arr에 Pair<int, int>의 형태로 {입력 % K, 자리수}를 저장합니다.
arr[0] = {4, 1}
arr[1] = {6, 2}
이제, 우리는 계산할 때 427의 수열을 만들었다면 27의 자리값 2를 이용해
4 * 10 ^ 2 + 27 = 427을 만들 수 있고,
274를 만들었다면
27 * 10 ^1 + 4 = 274를 만들어 계산할 수 있습니다.
그렇다면, 자리수에 따라서 10의 거듭제곱의 나머지를 계속 사용할 것인데,
매번 자릿수 계산을 하는 것 보다는 아예 자릿수에 따른 K의 나머지를 저장해두는게 낫습니다.
Cache[i] = 10 ^ i 의 K에 대한 나머지를 저장합니다.
어차피 입력 자릿수는 50을 넘지 않으므로, 50칸의 cache를 미리 만들어 사용합시다.
이제 연산이 꽤나 깔끔해졌습니다.
다음은 DP 알고리즘입니다.
DP + 비트마스크 기법을 이용하여 문제를 풀 것입니다.
DP[비트][n] = 비트의 상황에서 n의 나머지를 가지는 수열의 갯수입니다.
예를들어, 위의 예시처럼 4와 27의 수열을 예로 들겠습니다.
비트 대응
11 = { 4, 27}
1. 4만 사용한 수열 4 % 7 == 4
DP[10][4] = 1
2. 27만 사용한 수열 27 % 7 = 6
DP[01][6] = 1
3. 4와 27을 모두 사용한 수열
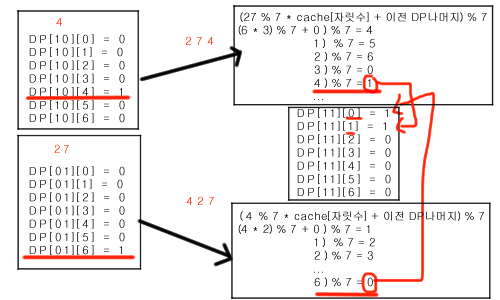
DP[10]의 모든 나머지 값에 따라 DP[11]에 더해줌
DP[01]의 모든 나머지 값에 따라 DP[11]에 더해줌
위와 같은 과정이 끝났으면,
DP[11111..][0]의 값과 총 입력값의 갯수를 기약 분수의 형태로 출력하면 정답입니다.
코드
#include <iostream>
#include <string>
#pragma warning(disable : 4996)
using namespace std;
//최대 공약수 구하는 함수
unsigned long long get_GCD(unsigned long long A, unsigned long long B)
{
while (B)
{
unsigned long long temp = A;
A = B;
B = temp % B;
}
return A;
}
//String의 K에 대한 나머지를 구함
int get_mod(string str, int K)
{
int n = 0;
for (char c : str)
{
n *= 10;
n += c - 48;
n %= K;
}
return n;
}
void solution(pair<int, int> *arr, int cache[], unsigned long long **&dp, int N, int K)
{
//현재 비트
for (int cur = 0; cur < (1 << N); cur++)
{
//현재 비트에서 추가해볼 비트
for (int i = 0; i < N; i++)
{
if (cur & (1 << i)) continue;
int next_bit = cur | (1 << i);
//추가된 비트의 나머지 연산
for (int j = 0; j < K; j++)
{
int next_K = ((j * cache[arr[i].second]) % K + arr[i].first) % K;
dp[next_bit][next_K] += dp[cur][j];
}
}
}
}
int main()
{
ios::sync_with_stdio(NULL);
cin.tie(NULL);
int N, K;
cin >> N;
//숫자 받기
string* inputs = new string[N];
for (int i = 0; i < N; i++) cin >> inputs[i];
cin >> K;
//동적할당
pair<int, int>* arr = new pair<int, int>[N];
int cache[51];
//DP 설정 DP[i][j] = i번째 비트의 나머지가 j인 수열의 갯수
unsigned long long** dp = new unsigned long long* [1 << N];
for (int i = 0; i < (1 << N); i++)
{
dp[i] = new unsigned long long[K];
fill_n(dp[i], K, 0);
}
dp[0][0] = 1;
//캐시 설정, 10 ^ i를 K로 나눈 나머지를 저장
cache[0] = 1 % K;
for (int i = 1; i < 51; i++) cache[i] = (cache[i - 1] * 10) % K;
//입력값의 K의 나머지만을 담아 arr에 보관
for (int i = 0; i < N; i++) arr[i] = { get_mod(inputs[i], K), inputs[i].size() };
delete[] inputs;
//풀기
solution(arr, cache, dp, N, K);
unsigned long long case_all = 1;
unsigned long long case_mine = dp[(1 << N) - 1][0];
//최대값 : 15! = 1307674368000 이므로 long long 사용
for (int i = 1; i < N + 1; i++) case_all *= i;
//기약 분수 형태로 나타내기 위한 과정
unsigned long long div = get_GCD(case_all, case_mine);
case_all /= div;
case_mine /= div;
printf("%lld/%lld", case_mine, case_all);
for (int i = 0; i < 1 << N; i++) delete[] dp[i];
delete[] dp;
}
그 외
cin을 더 선호하지만, scanf가 수행시간이 빨라 코딩 연습에는 더 많이 사용하고 있습니다만, scanf는 string을 담는 데에는 자유롭지 못한 점도 있고, 실무에서는 사용하지 않기 때문에 어떻게 입력을 받을 지에 대해 고민 중입니다.
cin.tie(NULL) 등의 방법을 이용해야 할까요?
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 5670번 문제 (0) | 2021.12.03 |
|---|---|
| [C++]백준 - 16637번 문제 (0) | 2021.12.03 |
| [C++]백준 - 9095번 문제 (0) | 2021.12.02 |
| [C++]백준 - 1764번 문제 (0) | 2021.12.01 |
| [C++]백준 - 16112번 문제 (0) | 2021.12.01 |
![[C++]백준 - 1086번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FNPzAl%2FbtrmTbSAsC9%2FeTSrudbptk3shjSFhzgpH0%2Fimg.jpg)