11438번: LCA 2
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정
www.acmicpc.net
11438번 : LCA 2
N(2 ≤ N ≤ 100,000)개의 정점으로 이루어진 트리가 주어진다. 트리의 각 정점은 1번부터 N번까지 번호가 매겨져 있으며, 루트는 1번이다.
두 노드의 쌍 M(1 ≤ M ≤ 100,000)개가 주어졌을 때, 두 노드의 가장 가까운 공통 조상이 몇 번인지 출력한다.
입력
첫째 줄에 노드의 개수 N이 주어지고, 다음 N-1개 줄에는 트리 상에서 연결된 두 정점이 주어진다. 그 다음 줄에는 가장 가까운 공통 조상을 알고싶은 쌍의 개수 M이 주어지고, 다음 M개 줄에는 정점 쌍이 주어진다.
출력
M개의 줄에 차례대로 입력받은 두 정점의 가장 가까운 공통 조상을 출력한다.

생각해 볼 점
LCA 문제입니다.
트리 문제를 다룰 때, 최송 공통 조상을 어떻게 찾을 것인가에 대하여,
우리는 DP처럼 모든 조상을 저장하여 빠르게 공통 조상을 찾아낼 수 있습니다.
참고에 좋은 링크를 하나 첨부하겠습니다.
최소 공통 조상(Lowest Common Ancestor) (수정: 2019-08-31) : 네이버 블로그 (naver.com)
최소 공통 조상(Lowest Common Ancestor) (수정: 2019-08-31)
징글징글한 그래프 파트가 일단은 끝났고, 트리에 관한 걸 조금 더 쓰려고 합니다. 그러나 스플레이 트리만...
blog.naver.com
우선, DP 문제는 아니지만 DP와 유사하게 생각해봅시다.
이차원 배열을 만들어서, 깊이에 따른 모든 부모를 저장해두면,
꽤 빠르게 공통 조상을 구할 수 있을 것입니다.

예를들어, 위와 같은 트리가 있고, 7번과 9번의 최소 공통조상을 찾고싶다면
우선, 노드마다 자신의 모든 부모를 저장합니다.
예시로 7번 노드와 9번 노드의 경우를 봅시다.
예시)
| 깊이 당 부모 | 0 | 1 | 2 | 3 |
| 노드 7 | 7 | 3 | 1 | 0 |
| 노드 9 | 9 | 4 | 1 | 0 |
예시 쿼리 : DP[7][1] == 3 (노드 7의 깊이 1 만큼 조상의 노드 번호)
루트 노드부터 내려오면서 부모가 달라지는 순간을 캐치하면 될 것입니다.
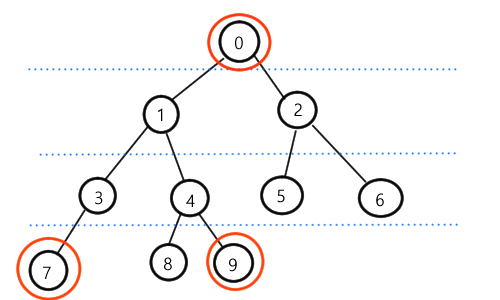


1번 노드 이후 부모가 서로 다르기 때문에, 그 윗 노드인 1번 노드가 최소 공통 조상이 됩니다.
이렇게 구현하면 행복하게 끝날 것 같지만, 아쉽게도 문제가 있습니다.
입력값이 무려 100000이나 됩니다.
그러면, 노드의 갯수가 1000000이고, 최악의 경우 저장 공간이
sizeof(int) * 100000 * 100000 씩이나 필요하게 됩니다.
이 저장공간을 감당할 수 없기 때문에, 우리는 Biniary Lifting이라는 기법을 사용할 것입니다.
* Binary Lifting이란?
2의 제곱수로 큰수를 압축합니다.
위의 방식대로 DP를 구축하면,
DP[7][0] ~ DP[7][3]까지 DP[7]의 배열은 4칸을 잡아먹습니다.
바이너리 리프팅을 사용하면 그럴 필요가 없습니다.
DP를 다음과 같이 수정해봅시다.
DP[N][i] = N번째 노드의 2 ^ i번째 조상
그러면, DP 배열은 아래 그림처럼 수정되겠죠

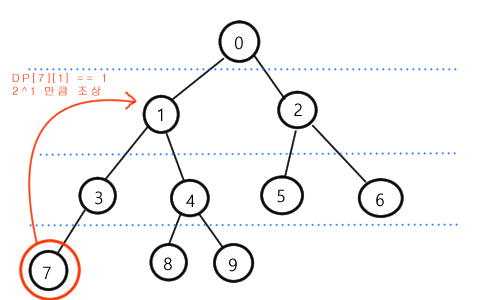
그러면, 깊이 3만큼 위의 조상은 어떻게 구해야 할까요?
DP[7][2]는 2^2만큼의 조상을 구하기 때문에 깊이 3보다 위의 조상을 구하게 됩니다.
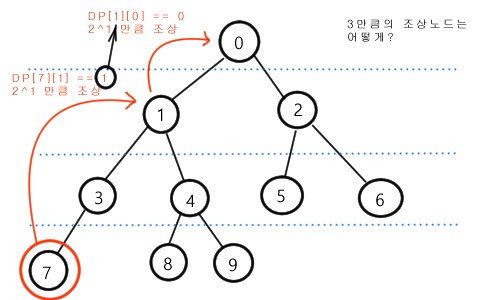
우선, DP[7][1]을 구하고,
남은 깊이 3 - 2 ^ 1 == 1 만큼 DP[7][1]의 조상을 구합니다.
그러면, 7번 노드의 깊이 3만큼 조상을 구할 수 있습니다.
이 방법을 사용하면, 기존에 100000 만큼의 공간을 더 써야했던 때와 달리
log2(100000) + 1 ==> 17만큼 밖에 안되는 저장 공간을 사용하므로
메모리 문제에서 상당히 프리해집니다.
기타 자세한 구현은 코드를 참고합시다.
코드
#include <iostream>
#include <cmath>
#include <vector>
using namespace std;
vector<int>* edges;
int** sparse;
int* level;
int N, M;
int logN;
//DFS 형식으로 Level과 sparse를 초기화
void set_level(int const& current)
{
for (int next_node : edges[current])
{
if (level[next_node] == -1)
{
sparse[next_node][0] = current;
level[next_node] = level[current] + 1;
set_level(next_node);
}
}
}
//스파스 테이블을 완성하는 함수
void set_sparse(int const& count)
{
if (count == logN) return;
for (int i = 0; i < N; i++)
{
if (sparse[i][count - 1] != -1)
sparse[i][count] = sparse[sparse[i][count - 1]][count - 1];
}
set_sparse(count + 1);
}
//parent를 구하는 함수
int get_parent(int const& node, int const &count)
{
if (count == 0) return node;
int A = int(log2(count));
int B = count - pow(2, A);
return get_parent(sparse[node][A], B);
}
int main()
{
scanf("%d", &N);
edges = new vector<int>[N];
sparse = new int* [N];
level = new int[N];
logN = int(log2(N)) + 1; //이진 리프팅
for (int i = 0; i < N; i++)
{
level[i] = -1;
sparse[i] = new int[logN];
fill_n(sparse[i], logN, -1);
}
level[0] = 0;
//에지 입력
for (int i = 0; i < N - 1; i++)
{
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
edges[a].push_back(b);
edges[b].push_back(a);
}
set_level(0);
set_sparse(1);
scanf("%d", &M);
//a와 b의 공통조상 찾기
for (int i = 0; i < M; i++)
{
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
//더 깊은 쪽이 b로 스왑
if (level[b] < level[a])
{
int temp = a;
a = b;
b = temp;
}
//b의 레벨을 a와 맞추어줌
b = get_parent(b, level[b] - level[a]);
int lv = level[a];
//공통조상 찾기
while (a != b)
{
int j = int(log2(lv));
for (; 0 < j; j--)
{
if (sparse[a][j] != sparse[b][j]) break;
}
a = sparse[a][j];
b = sparse[b][j];
}
printf("%d\n", a + 1);
}
for (int i = 0; i < N; i++) delete[] sparse[i];
delete[] edges;
delete[] level;
delete[] sparse;
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 13511번 문제 (0) | 2021.12.19 |
|---|---|
| [C++]백준 - 3176번 문제 (0) | 2021.12.19 |
| [C++]백준 - 1049번 문제 (0) | 2021.12.14 |
| [C++]백준 - 3584번 문제 (0) | 2021.12.13 |
| [C++]백준 - 7347번 문제 (0) | 2021.12.13 |
![[C++]백준 - 11438번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FcCV1Gd%2Fbtrn21bFEeB%2F922x13bN5HK5idLsZxbHBk%2Fimg.jpg)