7347번: 플립과 시프트
이 퍼즐은 m개의 검은색 원판과, n개의 흰색 원판으로 이루어진 임의의 수열(sequence)이 타원형 모양의 트랙에 배치되어 있는 구조입니다. 또 이 게임에서는 플립(flip)이라는 동작을 할 수 있는 디
www.acmicpc.net
7347번 : 플립과 시프트
이 퍼즐은 m개의 검은색 원판과, n개의 흰색 원판으로 이루어진 임의의 수열(sequence)이 타원형 모양의 트랙에 배치되어 있는 구조입니다. 또 이 게임에서는 플립(flip)이라는 동작을 할 수 있는 디스크를 이용할 수 있습니다. 플립은 임의의 세 연속된 디스크를 골라 그림과 같이 회전시켜서, 가운데 디스크는 그대로고 양 끝 디스크들의 위치를 바꾸는 동작을 말합니다. (Figure 1 참고) 플립을 할 때에는 트랙 위 어느 디스크를 중심으로도 회전시킬 수 있습니다.


m개의 검은색 원판과 n개의 흰색 원판으로 이루어진 수열이 주어질 때, 플립을 유한 번 수행하여 (Figure 2처럼) 검은색 원판은 검은색 원판끼리, 흰색 원판은 흰색 원판끼리 한 곳에 연속적으로 모여 있는 상태를 만들 수 있을지 없을지 판단하는 프로그램을 작성하세요.
입력
첫째 줄에 테스트 케이스의 개수 T가 주어집니다.
각 테스트 케이스는 한 줄로 이루어져 있습니다. 처음 주어진 수는 수열의 길이(10 ≤ m+n ≤ 30)이고, 그 다음 m개의 0(흰색 디스크)과 n개의 1(검은색 디스크)로 이루어진 수열이 주어집니다. m+n 은 10 이상 30 미만입니다. 또한 각각의 수는 공백으로 구분됩니다.
출력
각 테스트 케이스마다, 흰색과 검은색 디스크들을 분리해 낼 수 있으면 YES를, 아니면 NO를 한 줄에 출력합니다.

생각해 볼 점
구현 문제입니다.
한번 그려보면서 생각해보면 쉽습니다.

원형을 한번 펼쳐보면 저렇게 직선 형태로 원판이 담겨있습니다.
이제, 원판을 홀수, 짝수로 나누어서 담아봅시다.
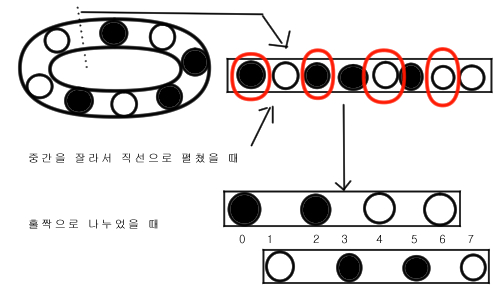
잘 생각해보면, 우리는 홀수 번째 원판은 홀수끼리,
짝수는 짝수끼리만 바꿀 수 있다는 걸 알 수 있습니다.
그러므로, 홀수 index와 짝수 index로 분리해서 담은 뒤,
검은 색 원판은 모두 한쪽으로 몰아버리면 분리가 가능한지 알 수 있습니다.
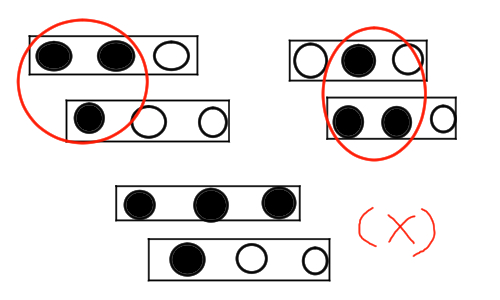
자, 그럼 판단을 해봅시다.
* 가능한 경우
1. 홀수의 검은색 갯수와 짝수의 검은색 갯수가 동일하다.
2. 홀수의 검은색 갯수가 짝수의 검은색 갯수보다 1개 많다.
3. 홀수의 검은색 갯수가 짝수의 검은색 갯수보다 1개 적다.
4. 총 원판의 갯수가 홀수개다.
* 불가능한 경우
1. 홀수의 검은색 갯수가 짝수의 검은색 갯수와 2개 이상 차이난다.
자, 그럼 가능한 경우의 4번은 왜 그럴까요?
총 원판의 갯수가 홀수개라면, 이런 문제가 생깁니다.
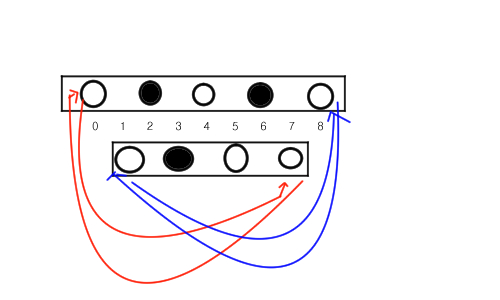
홀수와 짝수 index의 원판을 분리해두었는데, 양 끝에서 서로 교환이 가능합니다.
즉, 실제로 원판들을 바꿔보시면 금방 알 수 있듯이,
원판의 갯수가 홀수개면 어떤 입력을 받아도 무조건 흑백 분리가 가능합니다.
따라서, 우리는 실제로 배열 등을 써서 저 원판 돌리개를 구현할 필요가 없이
그냥 홀수, 짝수 번째 index의 검은 원판 갯수만 세서 정답을 출력할 수 있습니다.
코드
#include <iostream>
#include <cmath>
using namespace std;
int main()
{
int T;
scanf("%d", &T);
while (T--)
{
int N;
scanf("%d", &N);
int odd = 0;
int even = 0;
for (int i = 0; i < N; i++)
{
int input;
scanf("%d", &input);
if (input) i % 2 == 1 ? odd++ : even++;
}
//홀수개거나, 짝/ 홀 index 갯수차가 1 이하면 yes
if (N % 2 == 1 || abs(odd - even) <= 1) printf("YES\n");
else printf("NO\n");
}
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 1049번 문제 (0) | 2021.12.14 |
|---|---|
| [C++]백준 - 3584번 문제 (0) | 2021.12.13 |
| [C++]백준 - 1766번 문제 (0) | 2021.12.12 |
| [C++]백준 - 1005번 문제 (1) | 2021.12.11 |
| [C++]백준 - 3665번 문제 (0) | 2021.12.11 |
![[C++]백준 - 7347번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2Fwj1DP%2FbtrnN1WKKBr%2FWIy1cOqenHHgr9CD5Jrru0%2Fimg.jpg)