17386번: 선분 교차 1
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. 세 점이 일직선 위에 있는 경우는 없다.
www.acmicpc.net
17386번 : 선분 교차 1
2차원 좌표 평면 위의 두 선분 L1, L2가 주어졌을 때, 두 선분이 교차하는지 아닌지 구해보자.
L1의 양 끝 점은 (x1, y1), (x2, y2), L2의 양 끝 점은 (x3, y3), (x4, y4)이다.
입력
첫째 줄에 L1의 양 끝 점 x1, y1, x2, y2가, 둘째 줄에 L2의 양 끝 점 x3, y3, x4, y4가 주어진다. 세 점이 일직선 위에 있는 경우는 없다.
- -1,000,000 ≤ x1, y1, x2, y2, x3, y3, x4, y4 ≤ 1,000,000
- x1, y1, x2, y2, x3, y3, x4, y4는 정수
출력
L1과 L2가 교차하면 1, 아니면 0을 출력한다.
생각해 볼 점
CCW로 푸는것이 더 빠르고 효율적이지만, 저는 그냥 일차 함수 y = ax + b의 직선 공식에 대입해 풀었습니다.
A, B, C, D의 점을 받아, C와 D가 이루는 직선 Y = aX + B의 양측에 A와 B가 존재하는 지 알아봅니다.
Y > aX + b 이면, 양수 측 아니면 음수 측에 있음 / Y = aX + b가 성립하면 선 위에 있음
A, B를 넣어서
A.y - a * A.x - b랑
B.y - a * B.x - b가 부호가 다르면 성립합니다.
C와 D를 잇는 직선의 기울기 a = (D.y - C.y) / (D.x - C.x) 이고,
C 점에 대하여
Y = (D.y - C.y) * (X - C.x) / (D.x - C.x) + C.y가 성립할 것입니다. (Y = a * X의 평행이동)
이를 정리하면,
0 = (D.y - C.y) * (X - C.x) - (Y - C.y) * (D.x - C.x)일 것입니다.
0일 때 직선 위에 있는 것이므로
(X, Y)에 대입했을 때
(D.y - C.y) * (X - C.x) - (Y - C.y) * (D.x - C.x) > 0 이면, 이 직선보다 양수의 방향에 있으며
(D.y - C.y) * (X - C.x) - (Y - C.y) * (D.x - C.x) < 0 이면, 이 직선보다 음수의 방향에 있습니다.
이를 이용해서 선분의 교차를 파악하면 될 것 같습니다.
물론, 이를 한번만 하면
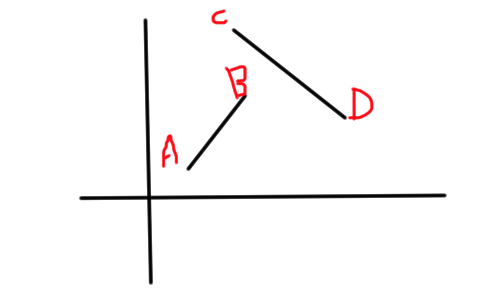
이 그림과 같은 경우를 판정하기에 무리가 있습니다.
따라서, 두번 수행합니다.
A, B의 직선 기준으로 C와 D는 양쪽 방향에 있으므로 만난다고 할 수 있지만,
C, D의 직선 기준으로 A와 B 점을 판정하면 둘다 양의 방향에 있으므로 만난다고 할 수 없습니다.
두 선의 경우를 모두 판정해야 정확한 결과를 얻을 수 있습니다.
코드
#include <iostream>
using namespace std;
//P1, P2의 두 점이 P3, P4가 만든 직선을 기준으로 각각 반대 방향에 있는지 검사
bool judge(pair<int, int> P1, pair<int, int> P2, pair<int, int> P3, pair<int, int> P4)
{
long long x_diff = P4.first - P3.first;
long long y_diff = P4.second - P3.second;
long long A = (P1.second - P3.second) * x_diff - (P1.first - P3.first) * y_diff;
long long B = (P2.second - P3.second) * x_diff - (P2.first - P3.first) * y_diff;
//오버플로우 경계
if(0 < A) A = 1;
else if(A < 0) A = -1;
if(0 < B) B = 1;
else if(B < 0) B = -1;
int result = A * B;
if(result <= 0) return true;
else return false;
}
int main()
{
pair<int, int> P1, P2, P3, P4;
cin >> P1.first >> P1.second >> P2.first >> P2.second;
cin >> P3.first >> P3.second >> P4.first >> P4.second;
//두번 수행하여 둘다 true면 교차 아니면 교차하지 않음
bool result = judge(P1, P2, P3, P4) & judge(P3, P4, P1, P2);
if(result) cout << 1;
else cout << 0;
return 0;
}
그 외
고집부리다가 이게 무슨 고생인지.. 그냥.. CCW로 풀걸 그랬습니다..
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 18111번 문제 (0) | 2021.10.22 |
|---|---|
| [C++]백준 - 17387번 문제 (0) | 2021.10.22 |
| [C++]백준 - 9372번 문제 (0) | 2021.10.20 |
| [C++]백준 - 9019번 문제 (0) | 2021.10.19 |
| [C++]백준 - 13913번 문제 (0) | 2021.10.19 |
![[C++]백준 - 17386번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FUuNnh%2FbtrikLTaCyi%2FzQW4PKXKy94PkWhhEqwQuk%2Fimg.jpg)