4803번: 트리
입력으로 주어진 그래프에 트리가 없다면 "No trees."를, 한 개라면 "There is one tree."를, T개(T > 1)라면 "A forest of T trees."를 테스트 케이스 번호와 함께 출력한다.
www.acmicpc.net
4803번 : 트리
그래프는 정점과 간선으로 이루어져 있다. 두 정점 사이에 경로가 있다면, 두 정점은 연결되어 있다고 한다. 연결 요소는 모든 정점이 서로 연결되어 있는 정점의 부분집합이다. 그래프는 하나 또는 그 이상의 연결 요소로 이루어져 있다.
트리는 사이클이 없는 연결 요소이다. 트리에는 여러 성질이 있다. 예를 들어, 트리는 정점이 n개, 간선이 n-1개 있다. 또, 임의의 두 정점에 대해서 경로가 유일하다.
그래프가 주어졌을 때, 트리의 개수를 세는 프로그램을 작성하시오.
입력
입력은 여러 개의 테스트 케이스로 이루어져 있다. 각 테스트 케이스의 첫째 줄에는 n ≤ 500과 m ≤ n(n-1)/2을 만족하는 정점의 개수 n과 간선의 개수 m이 주어진다. 다음 m개의 줄에는 간선을 나타내는 두 개의 정수가 주어진다. 같은 간선은 여러 번 주어지지 않는다. 정점은 1번부터 n번까지 번호가 매겨져 있다. 입력의 마지막 줄에는 0이 두 개 주어진다.
출력
입력으로 주어진 그래프에 트리가 없다면 "No trees."를, 한 개라면 "There is one tree."를, T개(T > 1)라면 "A forest of T trees."를 테스트 케이스 번호와 함께 출력한다.
생각해 볼 점
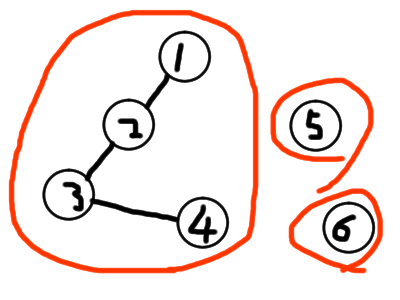
트리 문제이지만, 그래프의 탐색 과정에서 싸이클이 있는 지 확인하는 과정에 가깝습니다.
DFS 알고리즘을 통해, 싸이클이 있는 지 확인합니다.
싸이클이 존재하면, 이미 탐색된 노드를 한 번 더 탐색하게 될 것입니다.
DFS 도중 이미 탐색한 노드를 다시 들렀다면, 그 그래프는 트리의 형태가 아닙니다.
코드
#include <iostream>
#include <vector>
#include <stack>
using namespace std;
int main()
{
int TC = 1;
int N, M;
scanf("%d %d", &N, &M);
//입력이 0, 0 이면 종료
while(N != 0 || M != 0)
{
vector<int> *graph = new vector<int>[N];
bool *visited = new bool[N];
fill_n(visited, N, false);
//입력부
for(int i = 0; i < M; i++)
{
int a, b;
scanf("%d %d", &a, &b);
a--; b--;
graph[a].push_back(b);
graph[b].push_back(a);
}
stack<int> st;
int result = 0;
//모든 노드에서 한번씩 탐색 시도
for(int i = 0; i < N; i++)
{
st.push(i);
bool is_tree = true;
//DFS 알고리즘
while(!st.empty())
{
int current = st.top();
st.pop();
//순환이 있거나, 이미 탐색된 노드면 tree가 아님
if(visited[current])
{
is_tree = false;
continue;
}
for(int next : graph[current])
{
if(!visited[next]) st.push(next);
}
visited[current] = true;
}
if(is_tree) result++;
}
//출력부
printf("Case %d: ", TC);
switch(result)
{
case 0:
printf("No trees.\n");
break;
case 1:
printf("There is one tree.\n");
break;
default:
printf("A forest of %d trees.\n", result);
}
scanf("%d %d", &N, &M);
TC++;
delete[] visited;
delete[] graph;
}
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 6549번 문제 (0) | 2021.09.26 |
|---|---|
| [C++]백준 - 11723번 문제 (0) | 2021.09.25 |
| [C++]백준 - 5639번 문제 (0) | 2021.09.24 |
| [C++]백준 - 2263번 문제 (0) | 2021.09.24 |
| [C++]백준 - 14002번 문제 (0) | 2021.09.22 |
![[C++]백준 - 4803번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FDBzfX%2FbtrfRnHDpkh%2FwSeNrIJ4QnBH78iZmPDCX0%2Fimg.jpg)