1644번: 소수의 연속합
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
www.acmicpc.net
1644번 : 소수의 연속합
하나 이상의 연속된 소수의 합으로 나타낼 수 있는 자연수들이 있다. 몇 가지 자연수의 예를 들어 보면 다음과 같다.
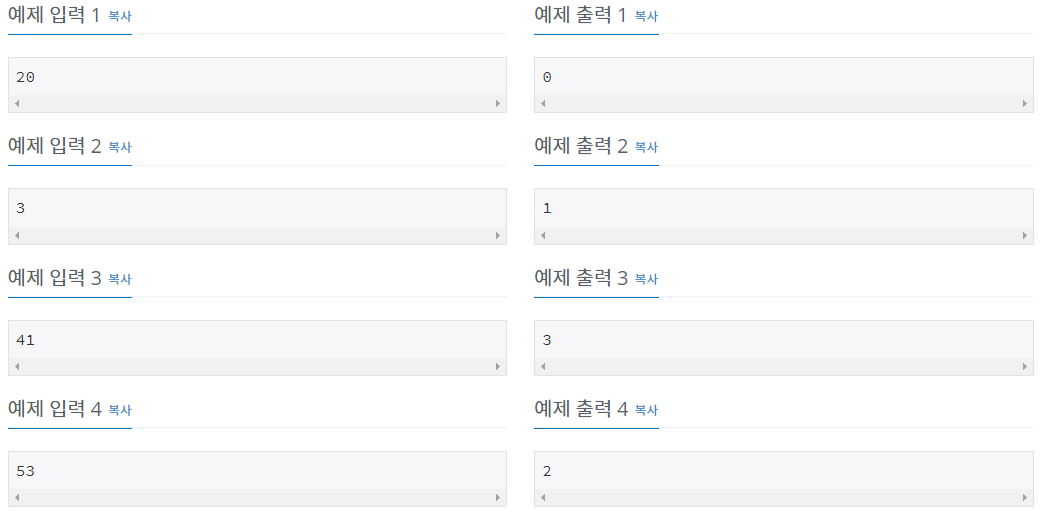
- 3 : 3 (한 가지)
- 41 : 2+3+5+7+11+13 = 11+13+17 = 41 (세 가지)
- 53 : 5+7+11+13+17 = 53 (두 가지)
하지만 연속된 소수의 합으로 나타낼 수 없는 자연수들도 있는데, 20이 그 예이다. 7+13을 계산하면 20이 되기는 하나 7과 13이 연속이 아니기에 적합한 표현이 아니다. 또한 한 소수는 반드시 한 번만 덧셈에 사용될 수 있기 때문에, 3+5+5+7과 같은 표현도 적합하지 않다.
자연수가 주어졌을 때, 이 자연수를 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 구하는 프로그램을 작성하시오.
입력
첫째 줄에 자연수 N이 주어진다. (1 ≤ N ≤ 4,000,000)
출력
첫째 줄에 자연수 N을 연속된 소수의 합으로 나타낼 수 있는 경우의 수를 출력한다.
생각해 볼 점
에라토스테네스의 체를 이용하여 2~N까지의 소수를 모두 벡터에 저장합니다.
저장된 소수를 투포인터 방식으로 탐색하여 경우의 수를 찾습니다.
소수를 저장한 배열 Prime을 지정하고 투포인터 Left, Right를 지정합니다.
Left ~ Right 인덱스를 모두 더한 값 summ을 기준으로 다음과 같이 진행합니다.
1. if(summ < N) -> right + 1, summ += Prime[right]
2. if(N < summ) -> left + 1, summ -= Prime[left]
3. if(N == summ) -> 경우의수 + 1, left + 1, summ -= Prime[left]
4. if(right == Prime_size) -> 알고리즘 종료
경우의 수를 출력합니다.
코드
#include <iostream>
#include <vector>
using namespace std;
int main()
{
int N;
cin >> N;
//1이하의 소수가 없으므로 예외처리
if(N == 1)
{
cout << 0;
return 0;
}
vector<int> prime;
//에라토스테네스의 체
bool *is_prime = new bool[N + 1];
fill_n(is_prime, N + 1, true);
for(int i = 2; i < N + 1; i++)
{
if(is_prime[i])
{
prime.push_back(i);
for(int j = i * 2; j < N + 1; j += i) is_prime[j] = false;
}
}
//투포인터
int len_prime = prime.size();
int left = -1;
int right = -1;
int summ = 0;
int result = 0;
while(right < len_prime)
{
if(summ < N)
{
right++;
summ += prime[right];
}
else if(summ > N)
{
left++;
summ -= prime[left];
}
else
{
left++;
right++;
summ += prime[right] - prime[left];
result++;
}
}
cout << result;
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 11725번 문제 (0) | 2021.09.18 |
|---|---|
| [C++]백준 - 12852번 문제 (0) | 2021.09.17 |
| [C++]백준 - 1806번 문제 (0) | 2021.09.14 |
| [C++]백준 - 1956번 문제 (0) | 2021.09.14 |
| [C++]백준 - 22993번 문제 (0) | 2021.09.12 |
![[C++]백준 - 1644번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F42qdE%2FbtrfnOLab1M%2FU4bkkdtcvP3XUp8Hm6lFIk%2Fimg.jpg)