1010번: 다리 놓기
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
www.acmicpc.net
1010번 : 다리 놓기
재원이는 한 도시의 시장이 되었다. 이 도시에는 도시를 동쪽과 서쪽으로 나누는 큰 일직선 모양의 강이 흐르고 있다. 하지만 재원이는 다리가 없어서 시민들이 강을 건너는데 큰 불편을 겪고 있음을 알고 다리를 짓기로 결심하였다. 강 주변에서 다리를 짓기에 적합한 곳을 사이트라고 한다. 재원이는 강 주변을 면밀히 조사해 본 결과 강의 서쪽에는 N개의 사이트가 있고 동쪽에는 M개의 사이트가 있다는 것을 알았다. (N ≤ M)
재원이는 서쪽의 사이트와 동쪽의 사이트를 다리로 연결하려고 한다. (이때 한 사이트에는 최대 한 개의 다리만 연결될 수 있다.) 재원이는 다리를 최대한 많이 지으려고 하기 때문에 서쪽의 사이트 개수만큼 (N개) 다리를 지으려고 한다. 다리끼리는 서로 겹쳐질 수 없다고 할 때 다리를 지을 수 있는 경우의 수를 구하는 프로그램을 작성하라.

입력
입력의 첫 줄에는 테스트 케이스의 개수 T가 주어진다. 그 다음 줄부터 각각의 테스트케이스에 대해 강의 서쪽과 동쪽에 있는 사이트의 개수 정수 N, M (0 < N ≤ M < 30)이 주어진다.
출력
각 테스트 케이스에 대해 주어진 조건하에 다리를 지을 수 있는 경우의 수를 출력한다.

생각해 볼 점
왼쪽에서 오른쪽으로 점과 점을 잇는 조합론입니다.
N과 M을 입력 받았을 때, N개의 왼쪽 점이 N개의 오른 쪽 점을 선택하는 것입니다.
이 때, 다리가 서로 교차가 안된다고 함은 곧 양쪽 점을 모두 선택 했을 때, 단 한가지 조합만을 만들 수 있음을 의미합니다.

우측 사진을 예로 들어봅시다.
좌측 4개의 점을 각각 1,2,3,4번 점이라 칭하고
우측 7개의 점을 각각 1,2,3,4,5,6,7이라 칭했을 때,
좌측의 점들이 각각 1,3,6,7 번을 선택했습니다.
만약 우측의 점 (1,3,6,7)번 집합에서 다른 경우의 수를 찾으려 한다면
어떤 경우에서든 다리는 서로 교차합니다.
좌측의 1번 점이 우측의 3번 점으로 이었을 때, 어떤 방법으로도
다리를 교차시키지 않고 우측의 점 (1,3,6,7)번으로 다리를 건설할 수 없습니다.
따라서, 순서가 상관 없는 조합의 문제입니다.
n C k 형태로 풀면 됩니다. 역시 두가지 방법으로 풀 수 있는데, 파스칼의 삼각형을 사용한 방법 혹은 그냥 조합식으로 푸는 방법이 있습니다.
만약 파스칼의 삼각형으로 푼다면, 재귀함수 + 동적 할당을 이용하여 구현하면 됩니다.
저는 조합식으로 풀겠습니다.
단, 조합식으로 풀 때 조심할 것이 있습니다.
입력 조건에서 받을 수 있는 최대 크기의 숫자가 30 C 15이므로, 평범하게 풀면 int 및 unsigned long long도 감당할 수 없습니다.
우선, k의 값이 2/N의 범위를 넘어간다면 N-k의 형태로 바꾸어 연산량을 줄이고,
반복문을 통해 계속 N-i / i + 1을 계속 곱해주도록 하겠습니다.
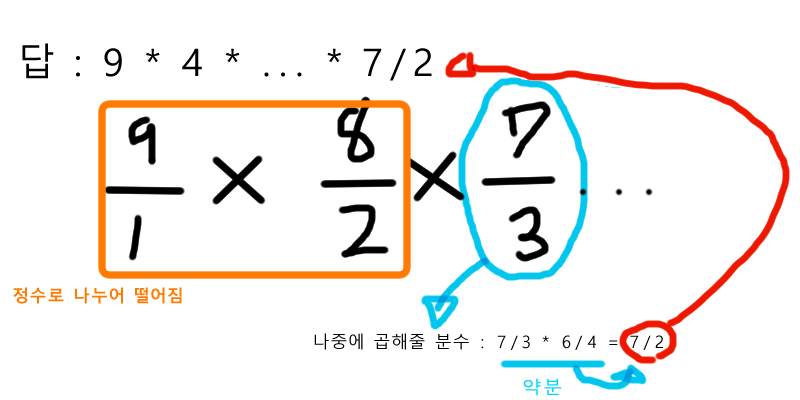
단, N-i / i + 1이 나누어 떨어지지 않을 경우, 따로 분수로 저장해 둔 후, 마지막에 곱해주겠습니다.
이 때에도 분수가 int 범위 값을 넘어가지 않도록 분모 분자의 최대공약수를 구해서 약분한 형태로 저장하겠습니다.
아래는 10 C 4의 예시입니다.
코드
#include <iostream>
using namespace std;
#define swap(a, b) {int t = a; a = b; b = a;}
int gcd(int a, int b) //최대공약수 구하기
{
if(a < b) swap(a,b);
while(0 < b) //유클리드 호제법
{
int temp = b;
b = a % b;
a = temp;
}
return a;
}
int main()
{
int T;
cin >> T;
for(int i = 0; i < T; i++)
{
int left, right;
cin >> left >> right;
if(right / 2 < left) left = right - left; //nCk에서 k가 n/2를 넘을 경우 k = n - k
long long result = 1;
pair<int, int> left_over = make_pair(1,1); //<분자 / 분모>를 저장하는 pair
for(int j = 0; j < left; j++)
{
if((right - j) % (j + 1) == 0) result *= (right - j) / (j + 1);
else //분수가 나누어 떨어지지 않으면 약분해서 저장함
{
left_over.first *= right-j;
left_over.second *= j+1;
int g = gcd(left_over.first, left_over.second);
left_over.first /= g;
left_over.second /= g;
}
}
result *= left_over.first; //따로 저장해둔 분수를 곱해 줌
result /= left_over.second;
cout << result << "\n";
}
return 0;
}
그 외
실무에서도 매우 큰 수는 자주 사용될 수 있는데, long long으로도 감당이 안되는 천문학적인 숫자들은 어떻게 다루게 될지 궁금하네요.
P.S : 분수를 다루게 될 경우 절대로 double 등을 사용해서 곱셈 나눗셈 연산을 하시면 안됩니다. double이 비교적 정확한 편이긴 하지만, 실제로 출력해볼 경우 값이 다른 경우를 심심찮게 볼 수 있을 겁니다. 반드시 정수로 해결하세요.
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 1676번 문제 (0) | 2021.06.10 |
|---|---|
| [C++]백준 - 9375번 문제 (0) | 2021.06.10 |
| [C++]백준 - 11051번 문제 (0) | 2021.06.04 |
| [C++]백준 - 11050번 문제 (0) | 2021.06.04 |
| [C++]백준 - 18870번 문제 (0) | 2021.06.03 |
![[C++]백준 - 1010번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FdUfP52%2Fbtq6z4plpWB%2FFTmIkZkyCScgUmZ3nihvyK%2Fimg.jpg)