2482번: 색상환
첫째 줄에 N색상환에서 어떤 인접한 두 색도 동시에 선택하지 않고 K개의 색을 고를 수 있는 경우의 수를 1,000,000,003 (10억 3) 으로 나눈 나머지를 출력한다.
www.acmicpc.net
2482번 : 색상환
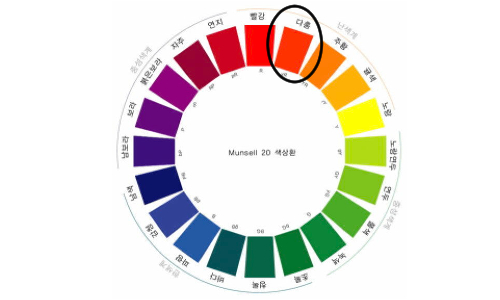
색을 표현하는 기본 요소를 이용하여 표시할 수 있는 모든 색 중에서 대표적인 색을 고리 모양으로 연결하여 나타낸 것을 색상환이라고 한다. 미국의 화가 먼셀(Munsell)이 교육용으로 고안한 20색상환이 널리 알려져 있다. 아래 그림은 먼셀의 20색상환을 보여준다.

그림 1. 먼셀의 20색상환
색상환에서 인접한 두 색은 비슷하여 언뜻 보면 구별하기 어렵다. 위 그림의 20색상환에서 다홍은 빨강과 인접하고 또 주황과도 인접하다. 풀색은 연두, 녹색과 인접하다. 시각적 대비 효과를 얻기 위하여 인접한 두 색을 동시에 사용하지 않기로 한다.
주어진 색상환에서 시각적 대비 효과를 얻기 위하여 서로 이웃하지 않은 색들을 선택하는 경우의 수를 생각해 보자. 먼셀의 20색상환에서 시각적 대비 효과를 얻을 수 있게 10개의 색을 선택하는 경우의 수는 2이지만, 시각적 대비 효과를 얻을 수 있게 11개 이상의 색을 선택할 수 없으므로 이 경우의 수는 0이다.
주어진 정수 N과 K에 대하여, N개의 색으로 구성되어 있는 색상환 (N색상환)에서 어떤 인접한 두 색도 동시에 선택하지 않으면서 서로 다른 K개의 색을 선택하는 경우의 수를 구하는 프로그램을 작성하시오.
입력
입력 파일의 첫째 줄에 색상환에 포함된 색의 개수를 나타내는 양의 정수 N(4 ≤ N ≤ 1,000)이 주어지고, 둘째 줄에 N색상환에서 선택할 색의 개수 K(1 ≤ K ≤ N)가 주어진다.
출력
첫째 줄에 N색상환에서 어떤 인접한 두 색도 동시에 선택하지 않고 K개의 색을 고를 수 있는 경우의 수를 1,000,000,003 (10억 3) 으로 나눈 나머지를 출력한다.

생각해 볼 점
직접 DP로 경우들을 구현하는 것 보다는 경우의 수 문제로 푸는 것이 좋습니다.
N 개의 색들 중 K개의 색을 먼저 뽑습니다.
예를 들어, 4개를 뽑는다고 생각하면, 4개의 색상 사이에 1개 이상의 색들을 넣습니다.
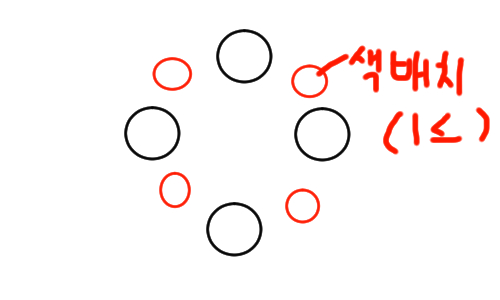
그런데, 우리는 배열 형태로 진행하므로 위의 원 배치를 직선으로 펼쳐봅시다.
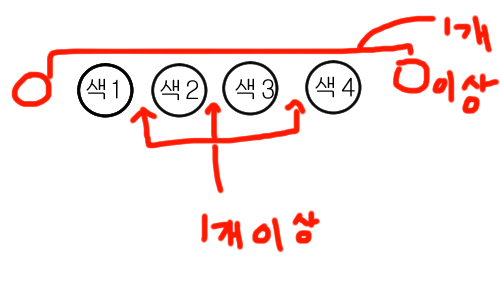
위와 같이 색배치가 이루어집니다.
그러면, 우선 N개의 색 중, K개는 이미 뽑을 색으로 빼놓았고,
K -1개는 사이사이에 반드시 넣어야 할 색으로 빠집니다.
그러면, 우리는 N개의 색중 K + K -1개의 색은 반드시 가져가야하므로 경우의 수로 고려하지 않아도 괜찮습니다.
그러므로, 우리는 N - 2K + 1개의 색을 어느자리에 배치할지 결정하기만 하면 됩니다.
총 K + 1개의 자리가 있고, N - 2K + 1개의 공을 넣는 경우의 수는
(K+1) H (N-2K+1)이죠.
예를 들어, 8개의 색 중 4개의 색을 뽑는다고 생각합시다.
이 중, 4개는 필수로 뽑힐 색,
3개는 위에서 뽑은 색 사이에 들어갈 색,
그러면 1개의 색을 5개의 공간 중 어디에 배치할 지 고민해야합니다.
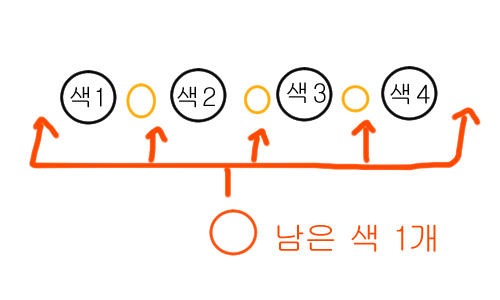
이 때, 5 H 1 = 5 C 1 = 5이므로, 5가지의 경우의 수가 있습니다.
그런데, 사실 위의 그림은 원형으로 이루어져 있다는 사실을 간과하였습니다.
따라서, 색1과 색4 사이에는 반드시 1개의 색상이 있어야합니다.
그러면, 색1의 좌측, 색4의 우측 중 한 곳에 색을 넣는 경우를 제외한 경우를 제거해 주어야 합니다.
그러면, 색1의 좌측과 색4를 제외하고 색이 들어간 경우를 빼줍니다.
3개의 공간에 1개의 색을 넣는 경우인
3 H 1 = 3 C 1 = 3이므로, 5 - 3 = 2가지 경우의 수가 답입니다.
결과적으로 답을 구하는 식은
(K + 1) H (N - 2K + 1) - (K - 1) H (N - 2K + 1)
입니다.
* 왜 K개의 색을 뽑을 때 N C K를 사용하지 않는가?
- 위의 색상환에서 빨강부터 0번 index로 시계방향으로 배열에 저장했다고 가정합니다.
예를 들어, 첫번 째 색을 뽑을 때, 첫번 째 색의 좌측에 색상을 배치하지 않았다면
첫번 째 색 = 빨강으로 시작합니다.
반면, 첫번째 색 왼쪽에 1개의 색을 배치하겠다고 할 경우, 다홍이 첫번째 색이 됩니다.
다홍 다음에 2개의 색을 두고 다음 색을 선택한다고 하면 노랑이 두번 째 색이 됩니다.
이런식으로, 어떤 색을 뽑을지가 아니라 뽑을 색 사이에 몇개의 색상 간격을 두느냐 만으로 색을 결정할 수 있으니
N C K는 필요하지 않습니다.
* N C K는 어떻게 계산하는가?
파스칼의 삼각형 - 위키백과, 우리 모두의 백과사전 (wikipedia.org)
파스칼의 삼각형 - 위키백과, 우리 모두의 백과사전
파스칼의 삼각형(Pascal's triangle)은 수학에서 이항계수를 삼각형 모양의 기하학적 형태로 배열한 것이다. 이것은 블레즈 파스칼에 의해 이름 붙여졌으나 이미 수세기 전에 다른 사람들에게서 연
ko.wikipedia.org
코드
#include <iostream>
using namespace std;
#define MOD 1000000003
int** dp;
//N C K를 계산하는 함수
int solution(int N, int K)
{
if (K < 0) return 0;
if (N < 2) return 1;
if (K == 0 || N == K) return 1;
if (dp[N][K]) return dp[N][K];
return dp[N][K] = (solution(N - 1, K) + solution(N - 1, K - 1)) % MOD;
}
int main()
{
int N, K;
cin >> N >> K;
dp = new int*[N + 1];
for (int i = 0; i < N + 1; i++)
{
dp[i] = new int[N + 1];
fill_n(dp[i], N + 1, 0);
}
//경우의 수 문제로 풀 경우,
//일자로 펼친 색상환에서 K개의 색상을 선택했을 때,
//선택된 K개의 색상들 사이 사이에 1개 이상의 색상을 넣었을 때의 경우의 수를 계산하면,
//N에서 선택된 K개의 색상과 사이에 넣은 K -1 개의 색상을 제외한 색상을
//K + 1개의 공간안에 넣는 경우의 수를 계산하는 것과 같다.
//즉, (K + 1) H (N - 2 * K + 1)의 경우를 계산한 후,
//양 끝에 0개의 색상을 넣은 경우(색상환이므로 조건에 위배되는 경우)를 제거하면,
//(K - 1) H (N - 2 * K + 1)을 위의 경우의 수에서 빼주면 정답이다.
//단, K - 1이 0보다 작은 경우에는 빼주지 않아야 한다.
//답 = (K + 1) H (N - 2 * K + 1) - (K - 1) H (N - 2 * K + 1)
int result_a = solution(N - K + 1, N - 2 * K + 1);
int result_b = 0;
if(K - 1) result_b = solution(N - K - 1, N - 2 * K + 1);
int result = result_a - result_b;
if (result < 0) result += MOD;
cout << result;
for (int i = 0; i < N + 1; i++) delete[] dp[i];
delete[] dp;
return 0;
}
그 외
'공부 및 정리 > 백준 코드' 카테고리의 다른 글
| [C++]백준 - 4354번 문제 (0) | 2021.11.18 |
|---|---|
| [C++]백준 - 1786번 문제 (0) | 2021.11.18 |
| [C++]백준 - 1032번 문제 (0) | 2021.11.17 |
| [C++]백준 - 1059번 문제 (0) | 2021.11.16 |
| [C++]백준 - 11004번 문제 (0) | 2021.11.16 |
![[C++]백준 - 2482번 문제](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2F6ONIX%2FbtrlfXRgZ85%2F60iohwofAcD6ygf6SIFmSk%2Fimg.jpg)